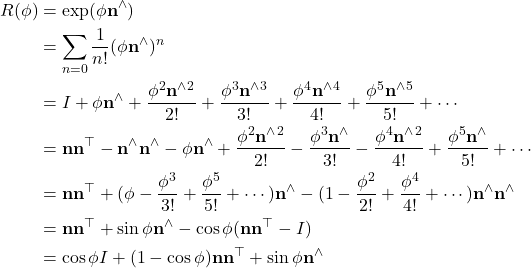The rotation matrix for rotating an object along normal direction ![]() with angle
with angle ![]() is given by
is given by
![]()
where 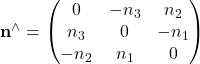 such that
such that ![]()
We can easily validate that the equation is correct, note that ![]() as desired. And for any vector
as desired. And for any vector ![]() perpendicular to
perpendicular to ![]()
![]() as desired as well.
as desired as well.
Compute 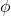 and
and  from
from 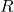
Note that ![]()
Thus, ![]() . Moreover, since
. Moreover, since ![]() , we can compute
, we can compute ![]() as the eigenvector of
as the eigenvector of ![]() .
.
Algebraic Derivation Rodrigues’ rotation formula
For any rotation matrix ![]() ,
, ![]() Thus
Thus ![]() is skew symmetric and can be written as
is skew symmetric and can be written as
![Rendered by QuickLaTeX.com \[\dot{R}R^\top=\begin{pmatrix}0 & n_3 & n_2\\n_3 &0 &-n_1\\-n_2&n_1&0 \end{pmatrix}={\bf n}^\wedge\Rightarrow \dot{R}={\bf n}^\wedge R\Rightarrow R(\phi) = \exp({\bf n}^\wedge \phi)\]](https://jiseung.site/wp-content/ql-cache/quicklatex.com-b0d91ef2963fe1afee280e271db55099_l3.png)
with 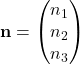 .
.
Note that we have ![]() and
and ![]() . Thus
. Thus
(1)