We can define ![Rendered by QuickLaTeX.com [{\bf a}]_\times = \begin{pmatrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{pmatrix}\triangleq {\bf a}^\wedge](https://jiseung.site/wp-content/ql-cache/quicklatex.com-eab2ccc13571924c00d1157eaf7bb159_l3.png)
![]()
Note that we have
![]() and
and
![]()
Triple product expansion
We will show the above with the triple product expansion: ![]()
Proof:
(1) 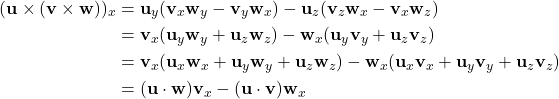
Similarly for the ![]() and
and ![]() components.
components. ![]()
Proof of 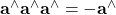
Note that for any ![]()
![]()
thus ![]()
![]()
Proof of 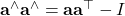
For any ![]()
(2) 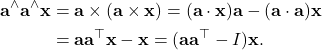
Thus, ![]()
![]()